Summary

Molecular Mechanics

Background

The "mechanical" molecular model was developed out of a need to describe molecular structures and properties in as practical a manner as possible. The range of applicability of molecular mechanics includes:

• Molecules containing thousands of atoms.
• Organics, oligonucleotides, peptides, and saccharides (metallo-organics and inorganics in some cases).
• Vacuum, implicit, or explicit solvent environments.
• Ground state only.
• Thermodynamic and kinetic (via molecular dynamics) properties.

The great computational speed of molecular mechanics allows for its use in procedures such as molecular dynamics, conformational energy searching, and docking, that require large numbers of energy evaluations.

Molecular mechanics methods are based on the following principles:

• Nuclei and electrons are lumped into atom-like particles.
• Atom-like particles are spherical (radii obtained from measurements or theory) and have a net charge (obtained from theory).
• Interactions are based on springs and classical potentials.
• Interactions must be preassigned to specific sets of atoms.
• Interactions determine the spatial distribution of atom-like particles and their energies.

Note how these principles differ from those of quantum mechanics.

The Anatomy of a Molecular Mechanics Force-Field

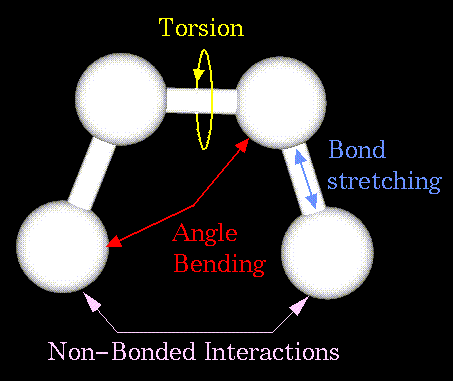
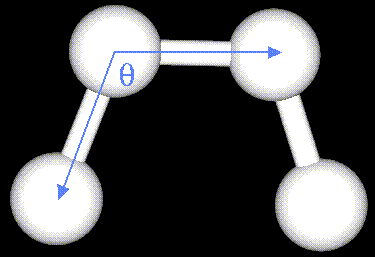
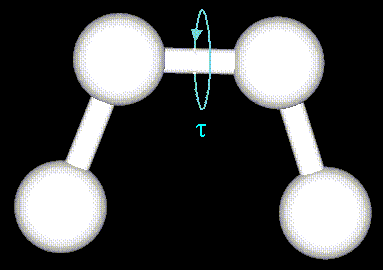
The mechanical molecular model considers atoms as spheres and bonds as springs.

Figure 60. The mathematics of spring deformation can be used to describe the ability of bonds to stretch, bend, and twist.

Non-bonded atoms (greater than two bonds apart) interact through van der Waals attraction, steric repulsion, and electrostatic attraction/repulsion. These properties are easiest to describe mathematically when atoms are considered as spheres of characteristic radii.

The object of molecular mechanics is to predict the energy associated with a given conformation of a molecule. However, molecular mechanics energies have no meaning as absolute quantities. Only differences in energy between two or more conformations have meaning. A simple molecular mechanics energy equation is given by:

    Energy =
        Stretching Energy +
        Bending Energy +
        Torsion Energy +
        Non-Bonded Interaction Energy

These equations together with the data (parameters) required to describe the behavior of different kinds of atoms and bonds, is called a force-field. Many different kinds of force-fields have been developed over the years. Some include additional energy terms that describe other kinds of deformations. Some force-fields account for coupling between bending and stretching in adjacent bonds in order to improve the accuracy of the mechanical model.

The mathematical form of the energy terms varies from force-field to force-field. The more common forms will be described.

Stretching Energy

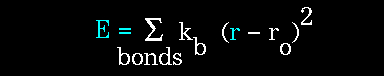
Figure 61.

Figure 62.

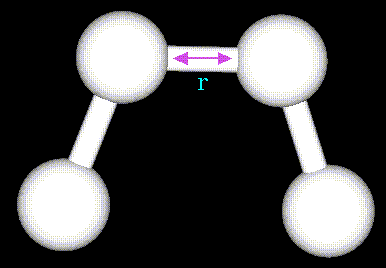
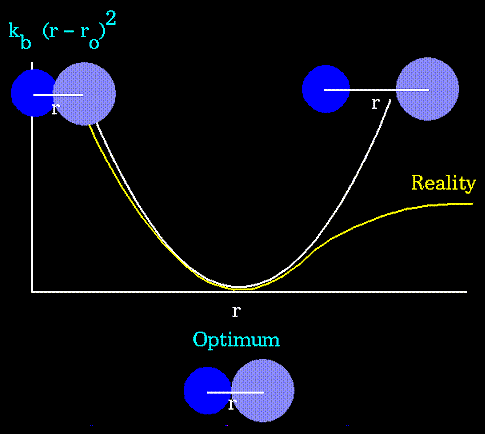
The stretching energy equation is based on Hooke's law. The "k_b" parameter controls the stiffness of the bond spring, while "r_o" defines its equilibrium length. Unique "k_b" and "r_o" parameters are assigned to each pair of bonded atoms based on their types (e.g. C-C, C-H, O-C, etc.). This equation estimates the energy associated with vibration about the equilibrium bond length. This is the equation of a parabola, as can be seen in the following plot:

Figure 63. Notice that the model tends to break down as a bond is stretched toward the point of dissociation.

Bending Energy

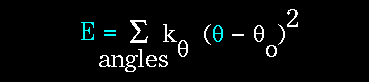
Figure 64.

Figure 65.

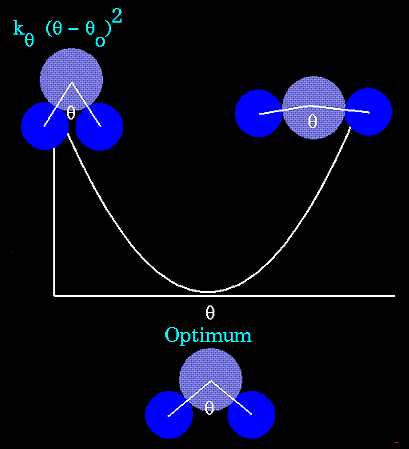
The bending energy equation is also based on Hooke's law. The "kθ" parameter controls the stiffness of the angle spring, while "θ₀" defines its equilibrium angle.

Figure 66. This equation estimates the energy associated with vibration about the equilibrium bond angle.

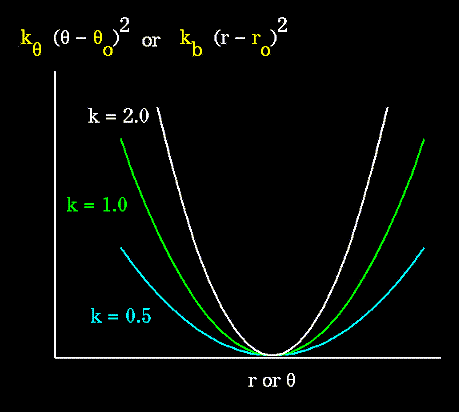
Unique parameters for angle bending are assigned to each bonded triplet of atoms based on their types (e.g. C-C-C, C-O-C, C-C-H, etc.). The effect of the "k_b" and "k_θ" parameters is to broaden or steepen the slope of the parabola. The larger the value of "k", the more energy is required to deform an angle (or bond) from its equilibrium value.

Figure 67. Shallow potentials are achieved for "k" values between 0.0 and 1.0. The Hookeian potential is shown in the following plot for three values of "k".

Torsion Energy

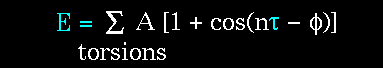
Figure 68.

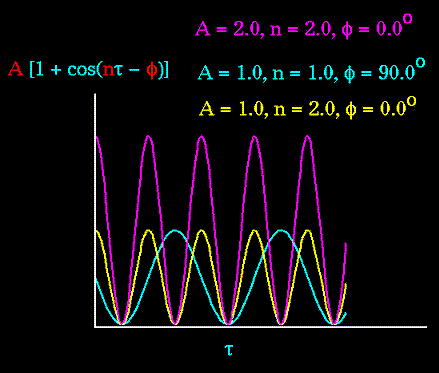
Figure 69. The torsion energy is modeled by a simple periodic function, as can be seen in this plot.

The torsion energy in molecular mechanics is primarily used to correct the remaining energy terms rather than to represent a physical process. The torsional energy represents the amount of energy that must be added to or subtracted from the Stretching Energy + Bending Energy + Non-Bonded Interaction Energy terms to make the total energy agree with experiment or rigorous quantum mechanical calculation for a model dihedral angle (ethane, for example might be used a a model for any H-C-C-H bond).

The "A" parameter controls the amplitude of the curve, the n parameter controls its periodicity, and "" shifts the entire curve along the rotation angle axis (tau). The parameters are determined from curve fitting. Unique parameters for torsional rotation are assigned to each bonded quartet of atoms based on their types (e.g. C-C-C-C, C-O-C-N, H-C-C-H, etc.). Torsion potentials with three combinations of "A", "n", and "" are shown in the following plot:

Figure 70.

Notice that "n" reflects the type symmetry in the dihedral angle. A CH₃-CH₃ bond, for example, ought to repeat its energy every 120 degrees. The cis conformation of a dihedral angle is assumed to be the zero torsional angle by convention. The parameter phi can be used to synchronize the torsional potential to the initial rotameric state of the molecule whose energy is being computed.

Non-Bonded Energy

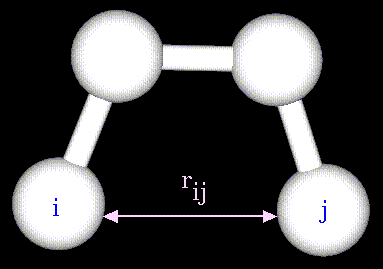
The non-bonded energy represents the pair-wise sum of the energies of all possible interacting non-bonded atoms i and j:

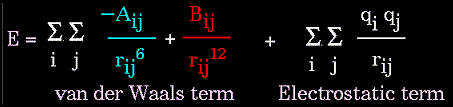
Figure 71.

Figure 72.

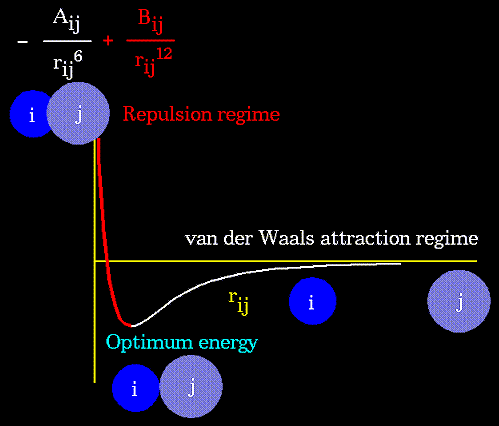
The non-bonded energy accounts for repulsion, Van der Waals attraction, and electrostatic interactions. Van der Waals attraction occurs at short range, and rapidly dies off as the interacting atoms move apart by a few Angstroms. Repulsion occurs when the distance between interacting atoms becomes even slightly less than the sum of their contact radii. Repulsion is modeled by an equation that is designed to rapidly blow up at close distances (1/r¹² dependency). The energy term that describes attraction/repulsion provides for a smooth transition between these two regimes. These effects are often modeled using a 6-12 equation, as shown in the following plot:

Figure 73.

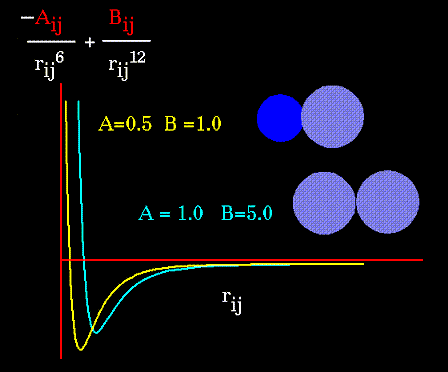
The "A" and "B" parameters control the depth and position (interatomic distance) of the potential energy well for a given pair of non-bonded interacting atoms (e.g. C:C, O:C, O:H, etc.). In effect, "A" determines the degree of "stickiness" of the van der Waals attraction and "B" determines the degree of "hardness" of the atoms (e.g marshmallow-like, billiard ball-like, etc.).

Figure 74.

The "A" parameter can be obtained from atomic polarizability measurements, or it can be calculated quantum mechanically. The "B" parameter is typically derived from crystallographic data so as to reproduce observed average contact distances between different kinds of atoms in crystals of various molecules.

The electrostatic contribution is modeled using a Coulombic potential. The electrostatic energy is a function of the charge on the non-bonded atoms, their interatomic distance, and a molecular dielectric expression that accounts for the attenuation of electrostatic interaction by the environment (e.g. solvent or the molecule itself). Often, the molecular dielectric is set to a constant value between 1.0 and 5.0. A linearly varying distance-dependent dielectric (i.e. 1/r) is sometimes used to account for the increase in environmental bulk as the separation distance between interacting atoms increases.

Partial atomic charges can be calculated for small molecules using an ab initio or semiempirical quantum technique (usually MOPAC or AMPAC). Some programs assign charges using rules or templates, especially for macromolecules. In some force-fields, the torsional potential is calibrated to a particular charge calculation method (rarely made known to the user). Use of a different method can invalidate the force-field consistency.

This document was obtained from the NIH.

Molecular Dynamics

In the broadest sense, molecular dynamics is concerned with molecular motion. Motion is inherent to all chemical processes. Simple vibrations, like bond stretching and angle bending, give rise to IR spectra. Chemical reactions, hormone-receptor binding, and other complex processes are associated with many kinds of intra- and intermolecular motions.

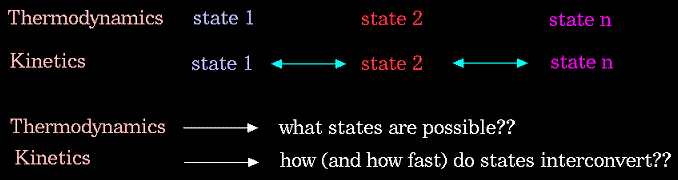
The driving force for chemical processes is described by thermodynamics. The mechanism by which chemical processes occur is described by kinetics. Thermodynamics dictates the energetic relationships between different chemical states, whereas the sequence or rate of events that occur as molecules transform between their various possible states is described by kinetics:

Figure 75.

Conformational transitions and local vibrations are the usual subjects of molecular dynamics studies. Molecular dynamics alters the intramolecular degrees of freedom in a step-wise fashion, analogous to energy minimization. The individual steps in energy minimization are merely directed at establishing a down-hill direction to a minimum. The steps in molecular dynamics, on the other hand, meaningfully represent the changes in atomic position, r_i, over time (i.e. velocity).

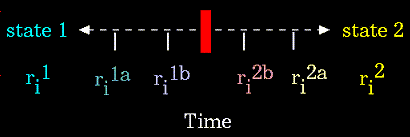
Figure 76. For the "ri" atoms of the system.

Figure 77. Newton's equation is used in the molecular dynamics formalism to simulate atomic motion.

The rate and direction of motion (velocity) are governed by the forces that the atoms of the system exert on each other as described by Newton's equation. In practice, the atoms are assigned initial velocities that conform to the total kinetic energy of the system, which in turn, is dictated by the desired simulation temperature. This is carried out by slowly "heating" the system (initially at absolute zero) and then allowing the energy to equilibrate among the constituent atoms. The basic ingredients of molecular dynamics are the calculation of the force on each atom, and from that information, the position of each atom throughout a specified period of time (typically on the order of picoseconds = 10^-12 seconds).

The force on an atom can be calculated from the change in energy between its current position and its position a small distance away. This can be recognized as the derivative of the energy with respect to the change in the atom's position:

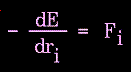
Figure 78.

Energies can be calculated using either molecular mechanics or quantum mechanics methods. Molecular mechanics energies are limited to applications that do not involve drastic changes in electronic structure such as bond making/breaking. Quantum mechanical energies can be used to study dynamic processes involving chemical changes. The latter technique is extremely novel, and of limited availability (CHARMM/GAMESS is an example of such a program).

Knowledge of the atomic forces and masses can then be used to solve for the positions of each atom along a series of extremely small time steps (on the order of femtoseconds = 10^-15 seconds). The resulting series of snapshots of structural changes over time is called a trajectory. The use of this method to compute trajectories can be more easily seen when Newton's equation is expressed in the following form:

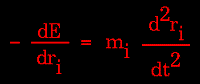
Figure 79.

In practice, trajectories are not directly obtained from Newton's equation due to lack of an analytical solution. First, the atomic accelerations are computed from the forces and masses. The velocities are next calculated from the accelerations based on the following relationship:

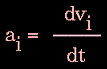
Figure 80.

Lastly, the positions are calculated from the velocities:

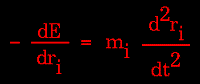
Figure 81.

In practice, trajectories are not directly obtained from Newton's equation due to lack of an analytical solution. First, the atomic accelerations are computed from the forces and masses. The velocities are next calculated from the accelerations based on the following relationship:

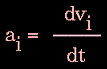
Figure 82.

Lastly, the positions are calculated from the velocities:

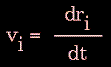
Figure 83.

A trajectory between two states can be subdivided into a series of sub-states separated by a small time step, "δt" (e.g. 1 femtosecond):

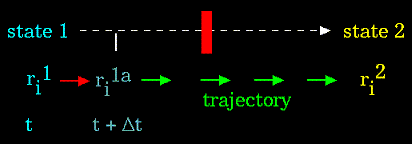
Figure 84.

The initial atomic positions at time "t" are used to predict the atomic positions at time "t + δt". The positions at "t + δt" are used to predict the positions at "t + 2*δt", and so on.

The "leapfrog" method is a common numerical approach to calculating trajectories based on Newton's equation. The steps can be summarized as follows:

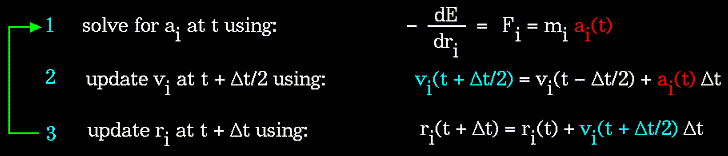
Figure 85.

The method derives its name from the fact that the velocity and position information successively alternate at 1/2 time step intervals.

Molecular dynamics has no defined point of termination other than the amount of time that can be practically covered. Unfortunately, the current picosecond order of magnitude limit is often not long enough to follow many kinds of state to state transformations, such as large conformational transitions in proteins.

Molecular dynamics calculations can be performed using AMBER, CHARMM, CHARMM/GAMESS, Discover, QUANTA/CHARMm, and SYBYL, but are done best with GROMACS or YASARA.

This document was obtained from the NIH. The above link is a dead link, and that is why I am glad I made a local copy (with permission).